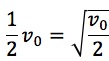【東大物理を解剖!】魔法のメガネ「重心」をかければ、難問もスッキリわかる!(大問1Ⅱ(1)(2))
サイエンストレーナーの桑子研です。毎日が実験!
東大物理2015を解く! 第1問Ⅰ(1)、(2)(3)、Ⅱ(1)(2) (3)(4) (5)(6)
「東大の入試問題」と聞くと、「自分には関係ない、難しすぎる世界…」なんて感じていませんか?でも、実はどんなに複雑に見える問題も、シンプルな物理法則の美しい組み合わせでできています。それはまるで、たった数種類のブロックから壮大なお城が作られるようなもの。
今回は、あの東京大学の物理の入試問題を題材に、一見難解な問題を「視点を変える」だけで驚くほどシンプルに解き明かす方法を一緒に探求していきましょう。使う道具は「重心」という魔法のメガネです。このメガネをかけると、複雑な2つの物体の運動が、まるで一つの物語のように見えてきますよ。
今回挑戦するのは、東大物理2015のⅡ(1)からです。この問題は、佐藤雅彦先生の「日常に潜む数理曲線」の動画からインスピレーションを得ると、より深く楽しめます。さあ、まずは問題の世界をのぞいてみましょう!
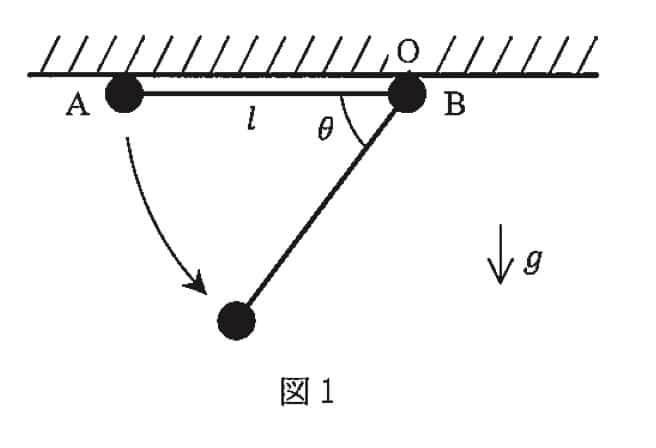


ステップ1:全体を1つの家族と見なす!- 重心の落下運動
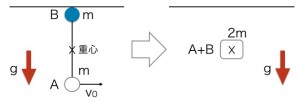
まず、手を離した瞬間の小球AとB。これらをバラバラに考えるのではなく、糸でつながれた「一心同体の1つの物体」と見なしてみましょう。この物体全体の動きを代表するのが「重心」です。重心とは、その物体の重さの中心点。まるで、この物体のリーダーのような存在ですね。
この「A・Bファミリー」全体に働く外からの力(外力)は何でしょうか?それは、地球が全体を引っ張る「重力」だけです(※)。だとすれば、このファミリーのリーダーである重心の動きは、ただのボールを空中で手放したときと同じ。つまり、重力加速度 g でまっすぐ下に落ちていくだけなのです。
これを運動方程式で表現すると、とてもシンプルになります。全体の質量は 2m なので、
(2m)a=2mg
a=g
ちなみに、小球AとBは同じ質量なので、重心の位置はちょうど糸のど真ん中になります。簡単でしょう?
ポイント!:内輪の力は無視する?
(※)「あれ?糸が引っ張る力(張力)はどこに行ったの?」と疑問に思った方、素晴らしい視点です!張力は、AとBがお互いに及ぼし合う力ですよね。このように、システム内部で作用し合う力を「内力」と呼びます。
2つの物体を「1つのファミリー」として見なした場合、この内力はファミリー内部でのやり取りに過ぎません。ファミリー全体が外に飛び出していく原因にはならないのです。だから、全体の動きを考えるときは、外から加わる力(外力)だけに着目すれば良い。これは物理の問題を解く上で非常に強力な「技」になります。例えば、運動量を考えるときにも、この「まとめて考える」アプローチが大活躍します。
ステップ2:重心に乗って世界を眺める! – 相対速度の不思議
さて、次に重心Gから見た各小球の動きを考えてみましょう。そのために、まずは手を離した瞬間の重心の速度を知る必要があります。ここで役立つのが「運動量保存則」という、もう一つの強力な法則です。「運動の勢いの合計は、外部から力が加わらない限り変わらない」というルールですね。
手を離す直前、小球Aは速さ v で運動しているので運動量は mv、小球Bは止まっているので運動量は 0 です。この合計が、合体した後の全体の運動量と等しくなります。重心の速度を V とすると、
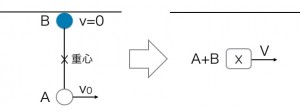
mv (Aの運動量) + 0 (Bの運動量) = (2m)V (A+B全体の運動量)
これを解くと、重心の速度 V=2vとなります(※1)。
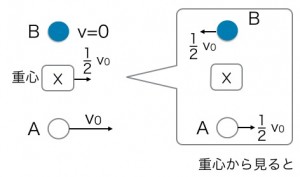
さあ、ここからが本番です!あなたが重心Gになったつもりで、AとBを眺めてみましょう。これは、ちょうど時速50kmで走る電車の中から、時速100kmで追い越していく新幹線と、駅に止まっている普通列車を見るようなものです。
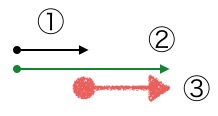
あなたは2vの速さで右に進んでいます。右向きに速さ v で動いているAは、あなたから見ると右向きに速さ2vで遠ざかって見えます。一方、止まっているBは、あなたから見ると左向きに速さ2vで遠ざかって見えるはずです(※2)。
これが相対速度です。重心から見ると、AとBは重心を中心にして、お互い反対方向に同じ速さでクルクルと回り始める、という美しい対称的な運動が見えてくるのです。
答え Aの相対速度は右向きに2v、Bの相対速度は左向きに2v
※1:円運動の知識を使うと、もっと直感的にわかります。Bを中心にAが円運動していたと考えると、糸の中心点である重心の速度は、円周上のAの速度のちょうど半分になりますね。
※2:計算でしっかり求めたい場合は、ベクトルの引き算を使います。「(相手の速度)-(自分の速度)」で計算できます。例えばGから見たAの相対速度は、
vAG=vA−vG=v−2v=2v
となります。
いかがでしたか? 「全体をまとめて見る」「重心の視点に立つ」という2つのステップで、東大の問題もスッキリと解き明かすことができました。物理は、このように物事を見る「解像度」を上げてくれる、とてもエキサイティングな学問なのです。
東大物理の目次へ戻る 第1問Ⅰ(1)、(2)(3)、Ⅱ(1)(2) (3)(4) (5)(6)
お問い合わせ・ご依頼について
科学の不思議やおもしろさをもっと身近に!自宅でできる楽しい科学実験や、そのコツをわかりやすくまとめています。いろいろ検索してみてください!
![]() 科学のネタチャンネルでは実験動画を配信中!
科学のネタチャンネルでは実験動画を配信中!